236. Триомино
Сколькими
способами можно замостить прямоугольник 2 × n триоминошками? Триомино – это геометрическая фигура, составленная
из трех квадратов, соединяющихся между собой вдоль полного ребра. Есть только
две возможных триоминошки:
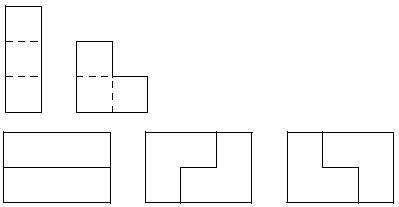
Например, замостить
прямоугольник 2 × 3 можно только тремя различными способами. Поскольку
ответ может быть достаточно большим, искомое количество способов следует
вычислять по модулю 106.
Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 100). Каждая из следующих t строк содержит значение n
(0 < n < 109).
Выход. Для каждого теста в отдельной строке выведите количество
способов, которыми можно замостить прямоугольник 2 × n. Результат следует выводить по модулю 106.
|
Пример
входа |
Пример
выхода |
|
3 3 4 6 |
3 0 11 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Обозначим через
Un количество способов
замостить прямоугольник 2 × n с
помощью триомино. Обозначим через Vn
количество способов замостить прямоугольник 2 × n без угла 1 × 1 с помощью триомино.
Имеем следующие
начальные соотношения:
U1=
0, U2 = 0, U3 = 3
V1 =
0, V2 = 1, V3 = 0
Рассмотрим
возможные способы замощения прямоугольников Un и Vn.

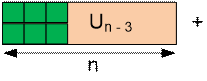



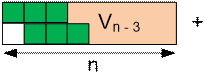
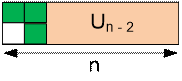
Получим
следующие рекуррентные соотношения:
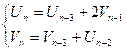
Исходя
из начальных условий, найдем U0 и V0:
 ,
,  ,
, 
Составим таблицу значений для Un и Vn:
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Un |
1 |
0 |
0 |
3 |
0 |
0 |
11 |
0 |
0 |
41 |
0 |
0 |
153 |
|
Vn |
0 |
0 |
1 |
0 |
0 |
4 |
0 |
0 |
15 |
0 |
0 |
56 |
0 |
Сдвинем вторую строку на две позиции
влево. Тогда столбцы для индексов, не кратных 3, будут содержать только нули.
Удалим их. Перенумеруем новые столбцы. Таблица примет вид:
|
n |
0 |
1 |
2 |
3 |
4 |
|
Un |
1 |
3 |
11 |
41 |
153 |
|
Vn |
1 |
4 |
15 |
56 |
209 |
Рекуррентные
соотношения перепишутся в виде:
 ,
, 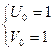
Или то же самое что
 ,
, 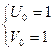
Рассмотрим
матрицу A = ![]() . A2 =
. A2 = ![]() , A3 =
, A3 = ![]() . Можно заметить, что первая строка матрицы An содержит значения Un-1
и Vn-1. Это
действительно так, потому что
. Можно заметить, что первая строка матрицы An содержит значения Un-1
и Vn-1. Это
действительно так, потому что
![]() *
* ![]() =
= ![]() =
= ![]()
Для решения задачи (нахождения значения Un) достаточно вычислить An+1 и вывести ее
элемент в левом верхнем углу. Возведение в степень совершаем за время O(log2n),
так как n < 109.
Все вычисления проводим по модулю 106.
Реализация алгоритма
Объявим модуль MOD, по которому будем проводить вычисления. Объявим класс
двумерной матрицы Matrix.
class Matrix
{
public:
long long a, b, c, d;
Matrix(long long a = 1, long long b = 0,
long long c = 0, long long d = 1)
{
this->a
= a; this->b = b;
this->c
= c; this->d = d;
}
Перегрузим оператор умножения матриц.
Matrix operator*
(const Matrix &x)
{
Matrix res;
res.a = (a * x.a + b * x.c) % MOD;
res.b = (a * x.b + b * x.d) % MOD;
res.c = (c * x.a + d * x.c) % MOD;
res.d = (c * x.b + d * x.d) % MOD;
return res;
}
Перегрузим оператор возведения
матрицы в степень n.
Matrix operator^
(int n)
{
Matrix res, x(*this);
while(n
> 0)
{
if (n
& 1) res = res * x;
n >>= 1;
x = x * x;
}
return res;
}
};
Возводим матрицу ![]() в степень n.
в степень n.
long long
Solve(long long
n)
{
Matrix res(1,1,2,3);
res = res^n;
return res.a;
}
Основная часть
программы. Читаем входные данные. Если значение n не делится на 3, то ответ 0. Иначе делим n на 3 и возводим матрицу ![]() в степень n + 1.
в степень n + 1.
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
if (n % 3)
{
printf("0\n");
continue;
}
n /= 3;
res = Solve(n+1);
printf("%d\n",res);
}

